Appendix A. Attributions
| Collection: Understanding Basic Music Theory |
| Edited by: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/col10363/1.3/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/2.0/ |
| Module: Understanding Basic Music Theory: Course Introduction |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m13685/1.7/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/2.0/ |
| Module: The Staff |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10880/2.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Clef |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10941/2.19/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Pitch: Sharp, Flat, and Natural Notes |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10943/2.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Key Signature |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10881/2.15/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Enharmonic Spelling |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11641/1.13/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Duration: Note Lengths in Written Music |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10945/2.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Duration: Rest Length |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11887/1.8/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Time Signature |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10956/2.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Meter in Music |
| Used here as: Meter |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12405/1.10/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Pickup Notes and Measures |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12717/1.7/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Dots, Ties, and Borrowed Divisions |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11888/1.9/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Syncopation |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11644/1.8/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Tempo |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11648/1.9/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Repeats and Other Musical Road Map Signs |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12805/1.7/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Dynamics and Accents in Music |
| Used here as: Dynamics and Accents |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11649/1.11/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Articulation |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11884/1.8/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Rhythm |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11646/1.7/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Timbre: The Color of Music |
| Used here as: Timbre |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11059/2.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Melody |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11647/1.10/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: The Textures of Music |
| Used here as: Texture |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11645/1.11/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Harmony |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11654/1.11/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: An Introduction to Counterpoint |
| Used here as: Counterpoint |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11634/1.9/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Range |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12381/1.9/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: What Kind of Music is That? |
| Used here as: Classifying Music |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11421/1.11/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Acoustics for Music Theory |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m13246/1.11/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Standing Waves and Musical Instruments |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12413/1.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Harmonic Series I: Timbre and Octaves |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m13682/1.9/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Octaves and the Major-Minor Tonal System |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10862/2.23/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Half Steps and Whole Steps |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10866/2.20/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Major Keys and Scales |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10851/2.25/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Minor Keys and Scales |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10856/2.22/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Interval |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10867/2.25/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Harmonic Series II: Harmonics, Intervals, and Instruments |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m13686/1.10/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: The Circle of Fifths |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10865/2.15/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Scales that aren't Major or Minor |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11636/1.19/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Triads |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10877/2.17/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Naming Triads |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10890/2.16/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Consonance and Dissonance |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11953/1.12/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Beyond Triads: Naming Other Chords |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11995/1.14/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Beginning Harmonic Analysis |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11643/1.20/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Cadence in Music |
| Used here as: Cadence |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m12402/1.13/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Form in Music |
| Used here as: Form |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10842/2.14/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Ear Training |
| By: CatherineSchmidt-Jones and RussellJones |
| URL: http://cnx.org/content/m12401/1.15/ |
| Copyright: CatherineSchmidt-Jones and RussellJones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Tuning Systems |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11639/1.23/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Modes and Ragas: More Than just a Scale |
| Used here as: Modes and Ragas |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m11633/1.14/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
| Module: Transposition: Changing Keys |
| By: CatherineSchmidt-Jones |
| URL: http://cnx.org/content/m10668/2.18/ |
| Copyright: CatherineSchmidt-Jones |
| License: http://creativecommons.org/licenses/by/3.0/ |
6.4. Transposition: Changing Keys*
Changing the key of a piece of music is called transposing the music. Music in a major key can be transposed to any other major key; music in a minor key can be transposed to any other minor key. (Changing a piece from minor to major or vice-versa requires many more changes than simple transposition.) A piece will also sound higher or lower once it is transposed. There are some ways to avoid having to do the transposition yourself, but learning to transpose can be very useful for performers, composers, and arrangers.
Here are the most common situations that may require you to change the key of a piece of music:
-
To put it in the right key for your vocalists. If your singer or singers are struggling with notes that are too high or low, changing the key to put the music in their range will result in a much better performance.
-
Instrumentalists may also find that a piece is easier to play if it is in a different key. Players of both bowed and plucked strings generally find fingerings and tuning to be easier in sharp keys, while woodwind and brass players often find flat keys more comfortable and in tune.
-
Instrumentalists with transposing instruments will usually need any part they play to be properly transposed before they can play it. Clarinet, French horn, saxophone, trumpet, and cornet are the most common transposing instruments.
In some situations, you can avoid transposition, or at least avoid doing the work yourself. Some stringed instruments - guitar for example - can use a capo to play in higher keys. A good electronic keyboard will transpose for you. If your music is already stored as a computer file, there are programs that will transpose it for you and display and print it in the new key. However, if you only have the music on paper, it may be easier to transpose it yourself than to enter it into a music program to have it transposed. So if none of these situations apply to you, it's time to learn to transpose.
If you play a chordal instrument (guitar, for example), you may not need to write down the transposed music. There are instructions below for transposing just the names of the chords.
If you would like to get started playing guitar, you can check out this guide on the best online Guitar methods.
There are four steps to transposition:
-
Choose your transposition.
-
Use the correct key signature.
-
Move all the notes the correct interval.
-
Take care with your accidentals.
Step 1: Choose Your Transposition
In many ways, this is the most important step, and the least straightforward. The transposition you choose will depend on why you are transposing. If you already know what transposition you need, you can go to step two. If not, please look at the relevant sections below first:
-
Are you rewriting the music for a transposing instrument?
-
Are you looking for a key that is in the range of your vocalist?
-
Are you looking for a key that is more playable on your instrument?
Step 2: Write the New Key Signature
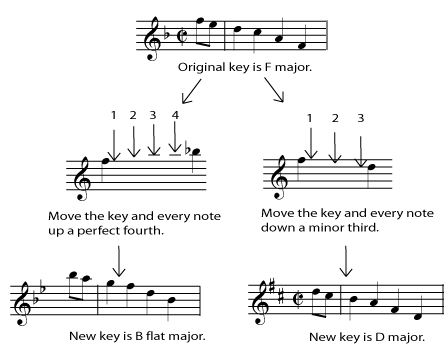
If you have chosen the transposition because you want a particular key, then you should already know what key signature to use. (If you don't, see Key Signature.) If you have chosen the transposition because you wanted a particular interval (say, a whole step lower or a perfect fifth higher), then the key changes by the same interval. For example, if you want to transpose a piece in D major up one whole step, the key also moves up one whole step, to E major. Transposing a piece in B minor down a major third will move the key signature down a major third to G minor. For more information on and practice identifying intervals, see Interval. For further information on how moving music up or down changes the key signature, see The Circle of Fifths.
Figure 6.15. Find the New Key

Step 3: Transpose the Notes
Now rewrite the music, changing all the notes by the correct interval. You can do this for all the notes in the key signature simply by counting lines and spaces. As long as your key signature is correct, you do not have to worry about whether an interval is major, minor, or perfect.
Figure 6.16. Move all the Notes
Step 4: Be Careful with Accidentals
Most notes can simply be moved the correct number of lines and spaces. Whether the interval is minor, major, or perfect will take care of itself if the correct key signature has been chosen. But some care must be taken to correctly transpose accidentals. Put the note on the line or space where it would fall if it were not an accidental, and then either lower or raise it from your new key signature. For example, an accidental B natural in the key of E flat major has been raised a half step from the note in the key (which is B flat). In transposing down to the key of D major, you need to raise the A natural in the key up a half step, to A sharp. If this is confusing, keep in mind that the interval between the old and new (transposed) notes (B natural and A sharp) must be one half step, just as it is for the notes in the key.
If you need to raise a note which is already sharp in the key, or lower a note that is already flat, use double sharps or double flats.
Figure 6.17. Transposing Accidentals

Exercise 6.4.1. (Go to Solution)
The best practice for transposing is to transpose a piece you know well into a new key.
Before you can begin transposing, you must decide what your new key will be. This will depend on why you are transposing, and what kinds of vocalists and instrumentalists you are working with.
Working with Vocalists
If you are trying to accomodate singers, your main concern in choosing a key is finding their range. Is the music you are working with too high or too low? Is it only a step too high, or does it need to be changed by a third or a fifth? Once you determine the interval needed, check to make certain this will be a comfortable key for your instrumentalists.
Example 6.1.
A church choir director wants to encourage the congregation to join in on a particular hymn. It is written in four parts with the melody in the soprano part, in a range slightly too high for untrained singers. The hymn is written in the key of E flat. Lowering it by a minor third (one and a half steps) will allow the congregation to sing with gusto.
Figure 6.18.
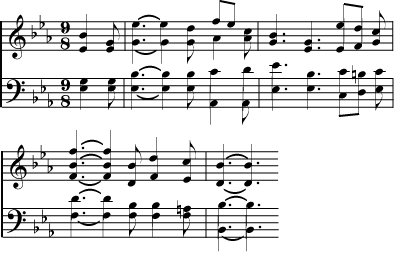
Figure 6.19.
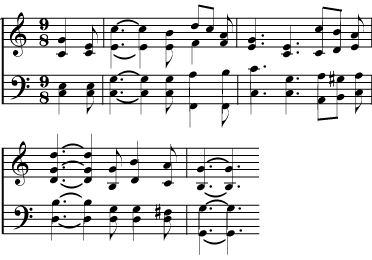
Example 6.2.
An alto vocalist would like to perform a blues standard originally sung by a soprano or tenor in B flat. She needs the song to be at least a whole step lower. Lowering it by a whole step would put it in the key of A flat. The guitar, bass, and harmonica players don't like to play in A flat, however, and the vocalist wouldn't mind singing even lower. So the best solution is to lower it by a minor third, and play in the key of G.
Figure 6.20.


Exercise 6.4.2. (Go to Solution)
You're accompanying a soprano who feels that this folk tune in C minor is too low for her voice. The guitar player would prefer a key with no flats and not too many sharps.
Figure 6.21.

Transposing Instruments
Transposing instruments are instruments for which standard parts are written higher or lower than they sound. A very accomplished player of one of these instruments may be able to transpose at sight, saving you the trouble of writing out a transposed part, but most players of these instruments will need a transposed part written out for them. Here is a short list of the most common transposing instruments. For a more complete list and more information, see Transposing Instruments.
Transposing Instruments
-
Clarinet is usually (but not always) a B flat instrument. Transpose C parts up one whole step for B flat instruments. (In other words, write a B flat part one whole step higher than you want it to sound.)
-
Trumpet and Cornet parts can be found in both B flat and C, but players with B flat instruments will probably want a B flat (transposed) part.
-
French Horn parts are usually in F these days. However, because of the instrument's history, older orchestral parts may be in any conceivable transposition, even changing transpositions in the middle of the piece. Because of this, some horn players learn to transpose at sight. Transpose C parts up a perfect fifth to be read in F.
-
Alto and Baritone Saxophone are E flat instruments. Transpose parts up a major sixth for alto sax, and up an octave plus a major sixth for bari sax.
-
Soprano and Tenor Saxophone are B flat instruments. Tenor sax parts are written an octave plus one step higher.
Why are there transposing instruments? Sometimes this makes things easier on instrumentalists; they may not have to learn different fingerings when they switch from one kind of saxophone to another, for example. Sometimes, as with piccolo, transposition centers the music in the staff (rather than above or below the staff). But often transposing instruments are a result of the history of the instrument. See the history of the French horn to find out more.
The transposition you will use for one of these instruments will depend on what type of part you have in hand, and what instrument you would like to play that part. As with any instrumental part, be aware of the range of the instrument that you are writing for. If transposing the part up a perfect fifth results in a part that is too high to be comfortable, consider transposing the part down a perfect fourth instead.
To Decide Transpositions for Transposing Instruments
-
Ask: what type of part am I transposing and what type of part do I want? Do you have a C part and want to turn it into an F part? Do you want to turn a B flat part into a C part? Non-transposing parts are considered to be C parts. The written key signature has nothing to do with the type of part you have; only the part's transposition from concert pitch (C part) matters for this step.
-
Find the interval between the two types of part. For example, the difference between a C and a B flat part is one whole step. The difference between an E flat part and a B flat part is a perfect fifth.
-
Make sure you are transposing in the correct direction. If you have a C part and want it to become a B flat part, for example, you must transpose up one whole step. This may seem counterintuitive, but remember, you are basically compensating for the transposition that is "built into" the instrument. To compensate properly, always transpose by moving in the opposite direction from the change in the part names. To turn a B flat part into a C part (B flat to C = up one step), transpose the part down one whole step. To turn a B flat part into an E flat part (B flat to E flat = down a perfect fifth), transpose the part up a perfect fifth.
-
Do the correct transposition by interval, including changing the written key by the correct interval.
Example 6.3.
Your garage band would like to feature a solo by a friend who plays the alto sax. Your songwriter has written the solo as it sounds on his keyboard, so you have a C part. Alto sax is an E flat instrument; in other words, when he sees a C, he plays an E flat, the note a major sixth lower. To compensate for this, you must write the part a major sixth higher than your C part.
Figure 6.22.


Example 6.4.
Your choral group is performing a piece that includes an optional instrumental solo for clarinet. You have no clarinet player, but one group member plays recorder, a C instrument. Since the part is written for a B flat instrument, it is written one whole step higher than it actually sounds. To write it for a C instrument, transpose it back down one whole step.
Figure 6.23.


Exercise 6.4.3. (Go to Solution)
There's a march on your community orchestra's program, but the group doesn't have quite enough trombone players for a nice big march-type sound. You have extra French horn players, but they can't read bass clef C parts.
Figure 6.24.

Playable Keys
Transposition can also make music easier to play for instrumentalists, and ease of playing generally translates into more satisfying performances. For example, someone writing a transcription for band of an orchestral piece may move the entire piece from a sharp key (easier for strings) to a nearby flat key (easier for winds). A guitar player, given a piece written in A flat for keyboard, will often prefer to play it in A or G, since the fingerings for chords in those keys are easier. Also, instrumentalists, like vocalists, have ranges that need to be considered.
Example 6.5.
Your eighth grade bassoon player would like to play a Mozart minuet at a school talent show with a flute-playing friend from band. The minuet is in C, but the melody is a little too low for a flute, and the bassoonist would also be more comfortable playing higher. If you transpose the whole piece up a minor third to E flat major, both players can hit the lowest notes, and you may also find that fingerings and tunings are better in the flat key.
Figure 6.25.


Exercise 6.4.4. (Go to Solution)
You've brought your guitar and your capo to the sing-along because you'd like to play along, too. Going through the music beforehand, you notice that your favorite song is in A flat. The pianist isn't prepared to play it in any other key, but you really don't like those thin-sounding chords in A flat. You can use your capo to raise the sound of your instrument (basically turning it into a transposing instrument in C sharp, D, D sharp, or even higher), but the less you raise it the more likely you are to still sound in tune with the piano.
Figure 6.26.

Transposing at sight means being able to read a part written in one key while playing it in another key. Like any other performance skill, it can be learned with practice, and it is a skill that will help you become an extremely versatile instrumentalist. (Vocalists transpose at sight without even thinking about it, since they don't have to worry about different fingerings.) To practice this skill, simply start playing familiar pieces in a different key. Since you know the piece, you will recognize when you make a mistake. Start with pieces written in C, and play them only a half step or whole step lower or higher than written. When this is easy, move on to more challenging keys and larger intervals. Practice playing in an unfamiliar clef, for example bass clef if you are used to reading treble clef. Or, if you play a transposing instrument, work on being able to play C parts on sight. You may find more opportunities to play (and earn the gratitude of your fellow musicians) if you can say, "we can change keys if you like", or "I can cover that bass clef C part for you, no problem."
If you are transposing entire chords, and you know the name of the chord, you may find it easier to simply transpose the name of the chord rather than transposing each individual note. In fact, transposing in this way is simple enough that even a musician who can't read music can do it.
Figure 6.27. Chromatic Circle
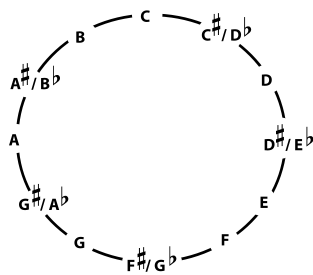
Step 1: Choose Your Transposition
Your choice of new key will depend on why you are transposing, but it may depend on other things, also.
-
If you are transposing because the music is too low or too high, decide how much higher or lower you want the music to sound. If you want the music to sound higher, go around the chromatic circle in the clockwise direction. If you want it lower, go in the counterclockwise direction. The further you go, the more it will change. Notice that, since you're going in a circle, raising the music a lot eventually gives the same chords as lowering it a little (and vice-versa). If some keys are easier for you to play in than others, you may want to check to make sure the key you choose has "nice" chords. If not, try another key near it.
-
If you are changing keys in order to make the chords easy to play, try changing the final chord so that it names an easy-to-play-in key. (Guitarists, for example, often find the keys G, D, A, E, C, Am, Em, and Dm easier to play in than other keys.) The last chord of most pieces will usually be the chord that names the key. If that doesn't seem to work for your piece, try a transposition that makes the most common chord an easy chord. Start changing the other chords by the same amount, and in the same direction, and see if you are getting mostly easy-to-play chords. While deciding on a new key, though, keep in mind that you are also making the piece higher or lower, and choose keys accordingly. A guitarist who wants to change chords without changing the pitch should lower the key (go counterclockwise on the circle) by as short a distance as possible to find a playable key. Then capo at the fret that marks the number of keys moved. For example, if you moved counterclockwise by three keys, put the capo at the third fret.
-
If you are changing keys to play with another instrumentalist who is transposing or who is playing in a different key from you, you will need to figure out the correct transposition. For a transposing instrument, look up the correct transposition (the person playing the instrument may be able to tell you), and move all of your chords up or down by the correct number of half steps. (For example, someone playing a B flat trumpet will read parts one step - two half steps - lower than concert pitch. So to play from the same part as the trumpet player, move all the chords counterclockwise two places.) If the instrumental part is simply written in a different key, find out what key it is in (the person playing it should be able to tell you, based on the key signature) and what key you are playing in (you may have to make a guess based on the final chord of the piece or the most common chord). Use the chromatic circle to find the direction and number of half steps to get from your key to the other key.
Step 2: Change the Names of All the Chords
Using the chromatic circle to count keys, change the note names in all of the chords by the same amount (the same number of half steps, or places in the chromatic circle) and in the same direction. Change only the note names (things like "F" and "C sharp" and "B flat"); don't change any other information about the chord (like major, minor, dim., 7, sus4, add11, etc.). If the bass note of the chord is written out as a note name, change that, also (using the same chromatic circle).
Check your transposition by playing it to see if it sounds right. If you don't like playing some of the chords in your new key, or if you have changed the key too much or not enough, try a different transposition.
Example 6.6.
Say you have a song in the key of G, which is too low for your voice. If it's just a little too low, you can go up two keys to A. If this is still too low, you can go up even further (5 keys altogether) to the key of C. Maybe that's high enough for your voice, but you no longer like the chords. If that is the case, you can go up two more keys to D. Notice that, because the keys are arranged in a circle, going up seven keys like this is the same as going down five keys.
Figure 6.28.
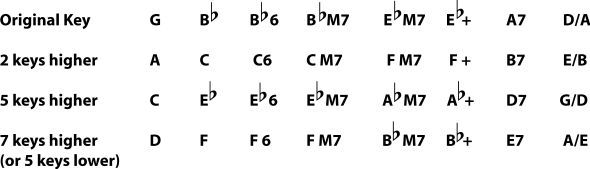
Example 6.7.
Now say you have a song in the key of E flat. It's not hard to sing in that key, so you don't want to go far, but you really don't like playing in E flat. You can move the song up one key to E, but you might like the chords even better if you move them down one key to D. Notice that if you are a guitar player, and everyone else really wants to stay in E flat, you can write the chords out in D and play them with a capo on the first fret; to everyone else it will sound as if you're playing in E flat.
Figure 6.29.

Exercise 6.4.5. (Go to Solution)
Now say that you have a song that is in B flat, which is more than a little (more than one key) too high for you. Find a key a bit lower that still has nice, easy-to-play chords for guitar.
Figure 6.30.

Solutions to Exercises
Solution to Exercise 6.4.1. (Return to Exercise)
Play the part you have transposed; your own ears will tell you where you have made mistakes.
Solution to Exercise 6.4.2. (Return to Exercise)
Transposing up a major third, to E minor, puts the song in a better range for a soprano, with a key signature that is easy for guitars.
Figure 6.31.

Solution to Exercise 6.4.3. (Return to Exercise)
The trombone part is in C in bass clef; the horn players are used to reading parts in F in treble clef. Transpose the notes up a perfect fifth and write the new part in treble clef.
Figure 6.32.


Solution to Exercise 6.4.4. (Return to Exercise)
Put the capo on the first fret to raise the sound by one half step. Then transpose the chords down one half step. You will be playing in G, a nice strong key for guitar, but sounding in A flat. For more on transposing chords, see Transposing Chord Names
Figure 6.33.

Solution to Exercise 6.4.5. (Return to Exercise)
The best solution here is probably to put the song in the key of G. This is three keys lower, and has easy chords.
Figure 6.34.

6.3. Modes and Ragas*
In many music traditions, including Western music, the list of all the notes that are expected or allowed in a particular piece of music is a scale. A long tradition of using scales in particular ways has trained listeners to expect certain things from a piece of music. If you hear a song in C major, for example, not only will your ear/brain expect to hear the notes from the C major scale, it will expect to hear them grouped into certain chords, and it will expect the chords to follow each other in certain patterns (chord progressions) and to end in a certain way (a cadence). You don't have to have any musical training at all to have these expectations; you only need to have grown up in a culture that listens to this kind of music.
The expectations for music in a minor key are a little different than for music in a major key. But it is important to notice that you can move that song in C major to E major, G flat major, or any other major key. It will sound basically the same, except that it will sound higher or lower. In the same way, all minor keys are so alike that music can easily be transposed from one minor key to another. (For more on this subject, see Major Scales, Minor Scales, Scales that aren't Major or Minor, and Transposition.)
This sameness is not true for musical traditions that use modes instead of scales. In these traditions, the mode, like a scale, lists the notes that are used in a piece of music. But each mode comes with a different set of expectations in how those notes will be used and arranged. This module introduces several traditions that are very different from each other, but that are all based on modes or ragas rather than on scales:
Although very different from each other, one thing that these disparate traditions share is that the modes or ragas that they are based on are much more variable than the major and minor scales of the tonal system. Figure 6.7 shows one example for comparison. The two major scales use different notes, but the relationship of the notes to each other is very similar. For example, the pattern of half steps and whole steps in each one is the same, and the interval (distance) between the tonic and the dominant is the same. Compare this to the two church modes. The pattern of whole steps and half steps within the octave is different; this would have a major effect on a chant, which would generally stay within the one octave range. Also, the interval between the finalis and the dominant is different, and they are in different places within the range of the mode. The result is that music in one mode would sound quite different than music in the other mode. You can't simply transpose music from one mode to another as you do with scales and keys; modes are too different.
Figure 6.7. Comparison of Scale and Mode

Figure 6.7 shows two scales and two modes. The two major scales use different notes, but the relationship of the notes to each other is very similar. For example, the pattern of half steps and whole steps in each one is the same, and the interval (distance) between the tonic and the dominant is the same. Compare this to the two church modes. The pattern of whole steps and half steps within the octave is different; this would have a major effect on a chant, which would generally stay within the one octave range. Also, the interval between the finalis and the dominant is different, and they are in different places within the range of the mode. The result is that music in one mode would sound quite different than music in the other mode. You can't simply transpose music from one mode to another as you do with scales and keys; modes are too different.
We don't have any recordings of ancient music, so we do not know exactly what it sounded like. But we can make some educated guesses as to what music from ancient Greek and Roman times really sounded like, based on their writings. We know, for example, that they used modes based on tetrachords, mini-scales of four notes, in descending pitch order, all contained within a stretch of a perfect fourth. We have very detailed descriptions of tetrachords and of Greek music theory (for example, Harmonics, written by Aristoxenus in the fourth century B.C.).
The perfect fourth is an interval that occurs naturally, for example in string and wind instrument harmonics (see Standing Waves and Musical Instruments for more on this), so we can be pretty certain that we understand that part of ancient Greek music theory. It is more difficult to be certain of the exact tuning of each note within a tetrachord. Enharmonic tetrachords are particularly confusing; it is clear that two of the notes were very close in pitch. As shown in Figure 6.8, they are often notated so that, using modern tuning, the two notes would sound the same. This sameness is a result of equal-tempered tuning, however; other tuning systems have been used which cause enharmonic notes to be tuned slightly differently. (See Tuning Systems for more about this.) It is not clear whether these ancient tetrachords actually had only three distinct pitches (it would not be the only time that something existed only to make a theory seem more consistent), or whether the two "enharmonic" notes were actually slightly different. References to "shading" in some of the ancient texts may have referred to differences in tuning.
Figure 6.8. Tetrachords

Since a tetrachord fills the interval of a perfect fourth, two tetrachords with a whole step between the end of one and the beginning of the other will fill an octave. Different Greek modes were built from different combinations of tetrachords.
Figure 6.9.

Western composers often consistently choose minor keys over major keys (or vice versa) to convey certain moods (minor for melancholy, for example, and major for serene). One interesting aspect of Greek modes is that different modes were considered to have very different effects, not only on a person's mood, but even on character and morality. This may also be another clue that ancient modes may have had more variety of tuning and pitch than modern keys do.
Sacred music in the middle ages in Western Europe - Gregorian chant, for example - was also modal, and the medieval church modes were also considered to have different effects on the listener. (As of this writing the site Ricercares by Vincenzo Galilei had a list of the "ethos" or mood associated with each medieval mode.) The names of the church modes were even borrowed from the names of the Greek modes, although the two systems don't really correspond to each other, or usemay have sounded more like some of the traditional raga-based Mediterranean and Middle Eastern musics (see below) than like medieval Western-European church music, and to avoid confusion some people prefer to name the church modes using Roman numerals.
Figure 6.10.

A mode can be found by playing all the "white key" notes on a piano for one octave. From D to D, for example is Dorian; from F to F is Lydian. Notice that no church modes began on A, B, or C. This is because a B flat was allowed, and the modes beginning on D, E, and F, when they use a B flat, have the same note patterns and relationships as would modes beginning on A, B, and C. After the middle ages, modes beginning on A, B, and C were named, but they are still not considered church modes. Notice that the Aeolian (or the Dorian using a B flat) is the same as an A (or D) natural minor scale and the Ionian (or the Lydian using a B flat) is the same as a C (or F) major scale.
Figure 6.11.
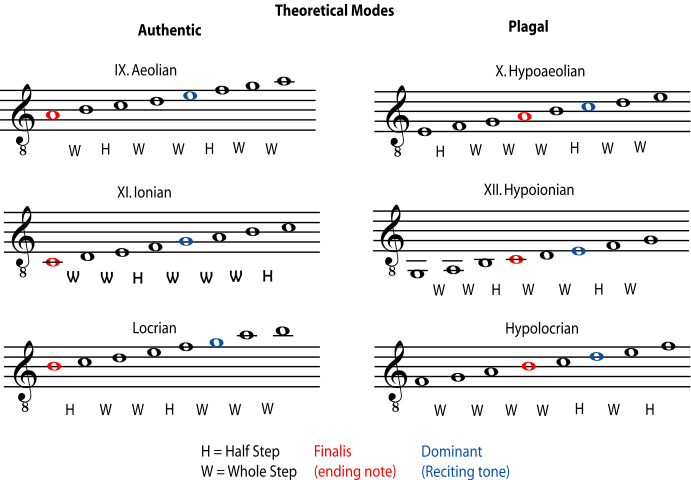
Each of these modes can easily be found by playing its one octave range, or ambitus, on the "white key" notes on a piano. But the Dorian mode, for example, didn't have to start on the pitch we call a D. The important thing was the pattern of half steps and whole steps within that octave, and their relationship to the notes that acted as the modal equivalent of tonal centers, the finalis and the dominant. Generally, the last note of the piece was the finalis, giving it the same "resting place" function as a modern tonic note. The dominant, also called the reciting tone or tenor, was the note most often used for long recitations on the same pitch.
The dominant in modal music did not have the harmonic function that the dominant has in tonal music. See harmonic analysis for a discussion of the dominant in modern music.
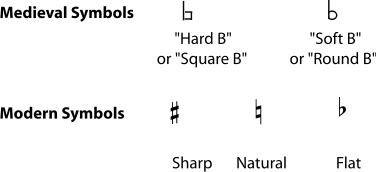
In our modern tonal system, any note may be sharp, flat, or natural, but in this modal system, only the B was allowed to vary. The symbols used to indicate whether the B was "hard" (our B natural) or "soft" (our B flat) eventually evolved into our symbols for sharps, flats, and naturals. All of this may seem very arbitrary, but it's important to remember that medieval mode theory, just like our modern music theory, was not trying to invent a logical system of music. It was trying to explain, describe, and systematize musical practices that were already flourishing because people liked the way they sounded.
Figure 6.12.
The tuning system used in medieval Europe was also not our familiar equal temperament system. It was a just intonation system, based on a pureperfect fifth. In this system, half steps are not all equal to each other. Slight adjustments are made in tuning and intervals to make them more pleasant to the ear; and the medieval ear had different preferences than our modern ears. This is another reason that modes sounded very different from each other, although that particular difference may be missing today when chant is sung using equal temperament.
Some jazz and folk music is also considered modal and also uses the Greek/medieval mode names. In this case, the scales used are the same as the medieval church modes, but they do not have a reciting tone and are used much more like modern major and minor scales. Modal European (and American) folk music tends to be older tunes that have been around for hundreds of years. Modal jazz, on the other hand, is fairly new, having developed around 1960.
It is important to remember when discussing these types of music that it does not matter what specific note the modal scale starts on. What matters is the pattern of notes within the scale, and the relationship of the pattern to the tonic/finalis. For example, note that the Dorian "scale" as written above starts on a D but basically has a C major key signature, resulting in the third and seventh notes of the scale being a half step lower than in a D major scale. (A jazz musician would call this flatted or flat thirds and sevenths.) So any scale with a flatted third and seventh can be called a Dorian scale.
Exercise 6.3.1. (Go to Solution)
You need to know your major keys and intervals to do this problem. Use the list of "white key" modes in Figure 6.10 to figure out the following information for each of the four modes below. Before looking at the solutions, check your own answers to make sure that the answers you get for step 2 and step 4 are in agreement with each other.
-
List the flats and sharps you would use if this were a major scale rather than a mode.
-
In this mode, which scale tones are raised or lowered from the major key?
-
What is the interval between the mode and the major key with the same key signature?
-
List the flats or sharps in this key signature.
-
Write one octave of notes in this mode. Check to make sure that your "modal scale" agrees with all the things that you have written about it already.
Example
-
D major has 2 sharps: F sharp and C sharp.
-
Looking at Figure 6.10, you can see that the Lydian mode starts on an F. The key of F major would have a B flat, but in the mode this is raised one half step, to B natural. Therefore the fourth degree of the Lydian mode is raised one half step.
-
F lydian has the same key signature as C major, which is a perfect fourth lower. So all Lydian modes have the same key signature as the major key a perfect fourth below them.
-
We want D Lydian. The major scale beginning a perfect fourth below D major is A major. A major has three sharps: F sharp, C sharp and G sharp. Adding a G sharp does raise the fourth degree of the scale by one half step, just as predicted in step 2.
Figure 6.13. Example: D Lydian

-
A Dorian
-
C Lydian
-
B flat Mixolydian
-
D Phrygian
The ragas of classical India and other, similar traditions, are more like modes than they are like scales. Like modes, different ragas sound very different from each other, for several reasons. They may have different interval patterns between the "scale" notes, have different expectations for how each note of the raga is to be used, and may even use slightly different tunings. Like the modal musics discussed above, individual Indian ragas are associated with specific moods.
In fact, in practice, ragas are even more different from each other than the medieval European modes were. The raga dictates how each note should be used, more specifically than a modal or major-minor system does. Some pitches will get more emphasis than others; some will be used one way in an ascending melody and another way in a descending melody; some will be used in certain types of ornaments. And these rules differ from one raga to the next. The result is that each raga is a collection of melodic scales, phrases, motifs, and ornaments, that may be used together to construct music in that raga. The number of possible ragas is practically limitless, and there are hundreds in common use. A good performer will be familiar with dozens of ragas and can improvise music - traditional classical music in India is improvised - using the accepted format for each raga.
The raga even affects the tuning of the notes. Indian classical music is usually accompanied by a tanpura, which plays a drone background. The tanpura is usually tuned to a pureperfect fifth, so, just as in medieval European music, the tuning system is a just intonation system. As in Western just intonation, the octave is divided into twelve possible notes, only some of which are used in a particular raga (just as Westerners use only some of the twelve notes in each key). But as was true for the church modes, using the pure perfect fifth means that some "half steps" will be larger than others. (If you would like to understand why this is so, please see Harmonic Series II and Tuning Systems.) Even though the variations between these different "half steps" are small, they strongly affect the sound of the music. So, the tuning of some of the notes (not the ones dictated by the tanpura) may be adjusted to better suit a particular raga. (Please see Listening to Indian Classical Music and Indian Classical Music: Tuning and Ragas for more information on this subject.)
To the average Western listener, medieval European chant and classical Indian music are the two most familiar traditions that are not based on major and minor scales. But many other musical traditions around the world are not based on Western scales. Some of these have modes similar to the medieval Church modes; they also tend to be a list of notes (or a pattern of intervals) used with a specific finalis, which may encourage certain types of melodies. While the church mode/jazz mode tradition features diatonic modes (which can be played using only the white keys of a piano), non-Western modes may use other types of scales.
In other music traditions, modes are much more like Indian ragas, featuring important variations in tuning and melodic expectations from one mode to the next, so that each mode may be seen as a collection of related melodic ideas, phrases, and ornamentations that are traditionally played with a certain set of notes tuned in a certain way. (Some non-Indian traditions even use the term raga.) All of these musics have long traditions that are very different from the familiar major-minor tonal system, and usually also have a different approach to harmony, rhythm, and performance practice.
Donald Jay Grout's A History of Western Music introduces both Greek and medieval modes. Lee Evans's Modes and Their Use in Jazz is both comprehensive and accessible for any musician who wants to begin to study that subject. For Western musicians, an introduction to ragas, that is neither too vague nor too technical, does not seem to be available as of this writing.
Solutions to Exercises
6.2. Tuning Systems*
The first thing musicians must do before they can play together is "tune". For musicians in the standard Western music tradition, this means agreeing on exactly what pitch (what frequency) is an "A", what is a "B flat" and so on. Other cultures not only have different note names and different scales, they may even have different notes - different pitches - based on a different tuning system. In fact, the modern Western tuning system, which is called equal temperament, replaced (relatively recently) other tuning systems that were once popular in Europe. All tuning systems are based on the physics of sound. But they all are also affected by the history of their music traditions, as well as by the tuning peculiarities of the instruments used in those traditions.
Do we have to choose just one tuning system? Join the discussion at Opening Measures
You will find below an introduction to a variety of tuning systems, including: Pythagorean, mean-tone, just intonation, well temperaments, equal temperament, and wide tuning.
To understand all of the discussion below, you must be comfortable with both the musical concept of interval and the physics concept of frequency. If you wish to follow the whole thing but are a little hazy on the relationship between pitch and frequency, the following may be helpful: Pitch; Acoustics for Music Theory; Harmonic Series I: Timbre and Octaves; and Octaves and the Major-Minor Tonal System. If you do not know what intervals are (for example, major thirds and perfect fourths), please see Interval and Harmonic Series II: Harmonics, Intervals and Instruments. If you need to review the mathematical concepts, please see Musical Intervals, Frequency, and Ratio and Powers, Roots, and Equal Temperament. Meanwhile, here is a reasonably nontechnical summary of the information below: Modern Western music uses the equal temperament tuning system. In this system, an octave (say, from C to C) is divided into twelve equally-spaced notes. "Equally-spaced" to a musician basically means that each of these notes is one half step from the next, and that all half steps sound like the same size pitch change. (To a scientist or engineer, "equally-spaced" means that the ratio of the frequencies of the two notes in any half step is always the same.) This tuning system is very convenient for some instruments, such as the piano, and also makes it very easy to change key without retuning instruments. But a careful hearing of the music, or a look at the physics of the sound waves involved, reveals that equal-temperament pitches are not based on the harmonics physically produced by any musical sound. The "equal" ratios of its half steps are the twelfth root of two, rather than reflecting the simpler ratios produced by the sounds themselves, and the important intervals that build harmonies can sound slightly out of tune. This often leads to some "tweaking" of the tuning in real performances, away from equal temperament. It also leads many other music traditions to prefer tunings other than equal temperament, particularly tunings in which some of the important intervals are based on the pure, simple-ratio intervals of physics. In order to feature these favored intervals, a tuning tradition may do one or more of the following: use scales in which the notes are not equally spaced; avoid any notes or intervals which don't work with a particular tuning; change the tuning of some notes when the key or mode changes.
Almost all music traditions recognize the octave. When note Y has a frequency that is twice the frequency of note Z, then note Y is one octave higher than note Z. A simple mathematical way to say this is that the ratio of the frequencies is 2:1. Two notes that are exactly one octave apart sound good together because their frequencies are related in such a simple way. If a note had a frequency, for example, that was 2.11 times the frequency of another note (instead of exactly 2 times), the two notes would not sound so good together. In fact, most people would find the effect very unpleasant and would say that the notes are not "in tune" with each other.
To find other notes that sound "in tune" with each other, we look for other sets of pitches that have a "simple" frequency relationship. These sets of pitches with closely related frequencies are often written in common notation as a harmonic series. The harmonic series is not just a useful idea constructed by music theory; it is often found in "real life", in the real-world physics of musical sounds. For example, a bugle can play only the notes of a specific harmonic series. And every musical note you hear is not a single pure frequency, but is actually a blend of the pitches of a particular harmonic series. The relative strengths of the harmonics are what gives the note its timbre. (See Harmonic Series II: Harmonics, Intervals and Instruments; Standing Waves and Musical Instruments; and Standing Waves and Wind Instruments for more about how and why musical sounds are built from harmonic series.)
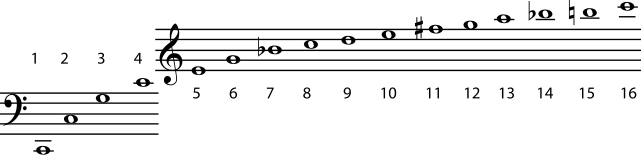
Figure 6.1. Harmonic Series on C
What does it mean to say that two pitches have a "simple frequency relationship"? It doesn't mean that their frequencies are almost the same. Two notes whose frequencies are almost the same - say, the frequency of one is 1.005 times the other - sound bad together. Again, anyone who is accustomed to precise tuning would say they are "out of tune". Notes with a close relationship have frequencies that can be written as a ratio of two small whole numbers; the smaller the numbers, the more closely related the notes are. Two notes that are exactly the same pitch, for example, have a frequency ratio of 1:1, and octaves, as we have already seen, are 2:1. Notice that when two pitches are related in this simple-ratio way, it means that they can be considered part of the same harmonic series, and in fact the actual harmonic series of the two notes may also overlap and reinforce each other. The fact that the two notes are complementing and reinforcing each other in this way, rather than presenting the human ear with two completely different harmonic series, may be a major reason why they sound consonant and "in tune".
Nobody has yet proven a physical basis for why simple-ratio combinations sound pleasant to us. For a readable introduction to the subject, I suggest Robert Jourdain's Music, the Brain, and Ecstasy
Notice that the actual frequencies of the notes do not matter. What matters is how they compare to each other - basically, how many waves of one note go by for each wave of the other note. Although the actual frequencies of the notes will change for every harmonic series, the comparative distance between the notes, their interval, will be the same.
For more examples, look at the harmonic series in Figure 6.1. The number beneath a note tells you the relationship of that note's frequency to the frequency of the first note in the series - the fundamental. For example, the frequency of the note numbered 3 in Figure 6.1 is three times the frequency of the fundamental, and the frequency of the note numbered fifteen is fifteen times the frequency of the fundamental. In the example, the fundamental is a C. That note's frequency times 2 gives you another C; times 2 again (4) gives another C; times 2 again gives another C (8), and so on. Now look at the G's in this series. The first one is number 3 in the series. 3 times 2 is 6, and number 6 in the series is also a G. So is number 12 (6 times 2). Check for yourself the other notes in the series that are an octave apart. You will find that the ratio for one octave is always 2:1, just as the ratio for a unison is always 1:1. Notes with this small-number ratio of 2:1 are so closely related that we give them the same name, and most tuning systems are based on this octave relationship.
The next closest relationship is the one based on the 3:2 ratio, the interval of the perfect fifth (for example, the C and G in the example harmonic series). The next lowest ratio, 4:3, gives the interval of a perfect fourth. Again, these pitches are so closely related and sound so good together that their intervals have been named "perfect". The perfect fifth figures prominently in many tuning systems. In Western music, all major and minor chords contain, or at least strongly imply, a perfect fifth. (See Triads and Naming Triads for more about the intervals in major and minor chords.)
Pythagorean Intonation
The Pythagorean system is so named because it was actually discussed by Pythagoras, the famous Greek mathematician and philosopher, who in the sixth century B.C. already recognized the simple arithmetical relationship involved in intervals of octaves, fifths, and fourths. He and his followers believed that numbers were the ruling principle of the universe, and that musical harmonies were a basic expression of the mathematical laws of the universe. Their model of the universe involved the "celestial spheres" creating a kind of harmony as they moved in circles dictated by the same arithmetical relationships as musical harmonies.
In the Pythagorean system, all tuning is based on the interval of the pure fifth. Pure intervals are the ones found in the harmonic series, with very simple frequency ratios. So a pure fifth will have a frequency ratio of exactly 3:2. Using a series of perfect fifths (and assuming perfect octaves, too, so that you are filling in every octave as you go), you can eventually fill in an entire chromatic scale.
Figure 6.2. Pythagorean Intonation

The main weakness of the Pythagorean system is that a series of pure perfect fifths will never take you to a note that is a pure octave above the note you started on. To see why this is a problem, imagine beginning on a C. A series of perfect fifths would give: C, G, D, A, E, B, F sharp, C sharp, G sharp, D sharp, A sharp, E sharp, and B sharp. In equal temperament (which doesn't use pure fifths), that B sharp would be exactly the same pitch as the C seven octaves above where you started (so that the series can, in essence, be turned into a closed loop, the Circle of Fifths). Unfortunately, the B sharp that you arrive at after a series of pure fifths is a little higher than that C.
So in order to keep pure octaves, instruments that use Pythagorean tuning have to use eleven pure fifths and one smaller fifth. The smaller fifth has traditionally been called a wolf fifth because of its unpleasant sound. Keys that avoid the wolf fifth sound just fine on instruments that are tuned this way, but keys in which the wolf fifth is often heard become a problem. To avoid some of the harshness of the wolf intervals, some harpsichords and other keyboard instruments were built with split keys for D sharp/E flat and for G sharp/A flat. The front half of the key would play one note, and the back half the other (differently tuned) note.
Pythagorean tuning was widely used in medieval and Renaissance times. Major seconds and thirds are larger in Pythagorean intonation than in equal temperament, and minor seconds and thirds are smaller. Some people feel that using such intervals in medieval music is not only more authentic, but sounds better too, since the music was composed for this tuning system.
More modern Western music, on the other hand, does not sound pleasant using Pythagorean intonation. Although the fifths sound great, the thirds are simply too far away from the pure major and minor thirds of the harmonic series. In medieval music, the third was considered a dissonance and was used sparingly - and actually, when you're using Pythagorean tuning, it really is a dissonance - but most modern harmonies are built from thirds (see Triads). In fact, the common harmonic tradition that includes everything from Baroque counterpoint to modern rock is often called triadic harmony.
Some modern Non-Western music traditions, which have a very different approach to melody and harmony, still base their tuning on the perfect fifth. Wolf fifths and ugly thirds are not a problem in these traditions, which build each mode within the framework of the perfect fifth, retuning for different modes as necessary. To read a little about one such tradition, please see Indian Classical Music: Tuning and Ragas.
Mean-tone System
The mean-tone system, in order to have pleasant-sounding thirds, takes rather the opposite approach from the Pythagorean. It uses the pure major third. In this system, the whole tone (or whole step) is considered to be exactly half of the pure major third. This is the mean, or average, of the two tones, that gives the system its name. A semitone (or half step) is exactly half (another mean) of a whole tone.
These smaller intervals all work out well in mean-tone tuning, but the result is a fifth that is noticeably smaller than a pure fifth. And a series of pure thirds will also eventually not line up with pure octaves, so an instrument tuned this way will also have a problem with wolf intervals.
As mentioned above, Pythagorean tuning made sense in medieval times, when music was dominated by fifths. Once the concept of harmony in thirds took hold, thirds became the most important interval; simple perfect fifths were now heard as "austere" and, well, medieval-sounding. So mean-tone tuning was very popular in Europe in the 16th through 18th centuries.
But fifths can't be avoided entirely. A basic major or minor chord, for example, is built of two thirds, but it also has a perfect fifth between its outer two notes (see Triads). So even while mean-tone tuning was enjoying great popularity, some composers and musicians were searching for other solutions.
Just Intonation
In just intonation, the fifth and the third are both based on the pure, harmonic series interval. Because chords are constructed of thirds and fifths (see Triads), this tuning makes typical Western harmonies particularly resonant and pleasing to the ear; so this tuning is often used (sometimes unconsciously) by musicians who can make small tuning adjustments quickly. This includes vocalists, most wind instruments, and many string instruments.
As explained above, using pure fifths and thirds will require some sort of adjustment somewhere. Just intonation makes two accommodations to allow its pure intervals. One is to allow inequality in the other intervals. Look again at the harmonic series.
Figure 6.3.

As the series goes on, the ratios get smaller and the notes closer together. Common notation writes all of these "close together" intervals as whole steps (whole tones) or half steps (semitones), but they are of course all slightly different from each other. For example, the notes with frequency ratios of 9:8 and 10:9 and 11:10 are all written as whole steps. To compare how close (or far) they actually are, turn the ratios into decimals.
Whole Step Ratios Written as Decimals
-
9/8 = 1.125
-
10/9 = 1.111
-
11/10 = 1.1
These are fairly small differences, but they can still be heard easily by the human ear. Just intonation uses both the 9:8 whole tone, which is called a major whole tone and the 10:9 whole tone, which is called a minor whole tone, in order to construct both pure thirds and pure fifths.
In case you are curious, the size of the whole tone of the "mean tone" system is also the mean, or average, of the major and minor whole tones.
The other accommodation with reality that just intonation must make is the fact that a single just-intonation tuning cannot be used to play in multiple keys. In constructing a just-intonation tuning, it matters which steps of the scale are major whole tones and which are minor whole tones, so an instrument tuned exactly to play with just intonation in the key of C major will have to retune to play in C sharp major or D major. For instruments that can tune almost instantly, like voices, violins, and trombones, this is not a problem; but it is unworkable for pianos, harps, and other other instruments that cannot make small tuning adjustments quickly.
As of this writing, there was useful information about various tuning systems at several different websites, including The Development of Musical Tuning Systems, where one could hear what some intervals sound like in the different tuning systems, and Kyle Gann's Just Intonation Explained, which included some audio samples of works played using just intonation.
There are times when tuning is not much of an issue. When a good choir sings in harmony without instruments, they will tune without even thinking about it. All chords will tend towards pure fifths and thirds, as well as seconds, fourths, sixths, and sevenths that reflect the harmonic series. Instruments that can bend most pitches enough to fine-tune them during a performance - and this includes most orchestral instruments - also tend to play the "pure" intervals. This can happen unconsciously, or it can be deliberate, as when a conductor asks for an interval to be "expanded" or "contracted".
But for many instruments, such as piano, organ, harp, bells, harpsichord, xylophone - any instrument that cannot be fine-tuned quickly - tuning is a big issue. A harpsichord that has been tuned using the Pythagorean system or just intonation may sound perfectly in tune in one key - C major, for example - and fairly well in tune in a related key - G major - but badly out of tune in a "distant" key like D flat major. Adding split keys or extra keys can help (this was a common solution for a time), but also makes the instrument more difficult to play. In Western music, the tuning systems that have been invented and widely used that directly address this problem are the various temperaments, in which the tuning of notes is "tempered" slightly from pure intervals. (Non-Western music traditions have their own tuning systems, which is too big a subject to address here. See Listening to Balinese Gamelan and Indian Classical Music: Tuning and Ragas for a taste of what's out there.)
Well Temperaments
As mentioned above, the various tuning systems based on pure intervals eventually have to include "wolf" intervals that make some keys unpleasant or even unusable. The various well temperament tunings that were very popular in the 18th and 19th centuries tried to strike a balance between staying close to pure intervals and avoiding wolf intervals. A well temperament might have several pure fifths, for example, and several fifths that are smaller than a pure fifth, but not so small that they are "wolf" fifths. In such systems, tuning would be noticeably different in each key, but every key would still be pleasant-sounding and usable. This made well temperaments particularly welcome for players of difficult-to-tune instruments like the harpsichord and piano.
Historically, there has been some confusion as to whether or not well temperament and equal temperament are the same thing, possibly because well temperaments were sometimes referred to at the time as "equal temperament". But these well temperaments made all keys equally useful, not equal-sounding as modern equal temperament does.
As mentioned above, mean-tone tuning was still very popular in the eighteenth century. J. S. Bach wrote his famous "Well-Tempered Klavier" in part as a plea and advertisement to switch to a well temperament system. Various well temperaments did become very popular in the eighteenth and nineteenth centuries, and much of the keyboard-instrument music of those centuries may have been written to take advantage of the tuning characteristics of particular keys in particular well temperaments. Some modern musicians advocate performing such pieces using well temperaments, in order to better understand and appreciate them. It is interesting to note that the different keys in a well temperament tuning were sometimes considered to be aligned with specific colors and emotions. In this way they may have had more in common with various modes and ragas than do keys in equal temperament.
Equal Temperament
In modern times, well temperaments have been replaced by equal temperament, so much so in Western music that equal temperament is considered standard tuning even for voice and for instruments that are more likely to play using just intonation when they can (see above). In equal temperament, only octaves are pure intervals. The octave is divided into twelve equally spaced half steps, and all other intervals are measured in half steps. This gives, for example, a fifth that is a bit smaller than a pure fifth, and a major third that is larger than the pure major third. The differences are smaller than the wolf tones found in other tuning systems, but they are still there.
Equal temperament is well suited to music that changes key often, is very chromatic, or is harmonically complex. It is also the obvious choice for atonal music that steers away from identification with any key or tonality at all. Equal temperament has a clear scientific/mathematical basis, is very straightforward, does not require retuning for key changes, and is unquestioningly accepted by most people. However, because of the lack of pure intervals, some musicians do not find it satisfying. As mentioned above, just intonation is sometimes substituted for equal temperament when practical, and some musicians would also like to reintroduce well temperaments, at least for performances of music which was composed with well temperament in mind.
In a way, equal temperament is also a compromise between the Pythagorean approach and the mean-tone approach. Neither the third nor the fifth is pure, but neither of them is terribly far off, either. Because equal temperament divides the octave into twelve equal semi-tones (half steps), the frequency ratio of each semi-tone is the twelfth root of 2. If you do not understand why it is the twelfth root of 2 rather than, say, one twelfth, please see the explanation below. (There is a review of powers and roots in Powers, Roots, and Equal Temperament if you need it.)
Figure 6.4.

In equal temperament, the only pure interval is the octave. (The twelfth power of the twelfth root of two is simply two.) All other intervals are given by irrational numbers based on the twelfth root of two, not nice numbers that can be written as a ratio of two small whole numbers. In spite of this, equal temperament works fairly well, because most of the intervals it gives actually fall quite close to the pure intervals. To see that this is so, look at Figure 6.5. Equal temperament and pure intervals are calculated as decimals and compared to each other. (You can find these decimals for yourself using a calculator.)
Figure 6.5. Comparing the Frequency Ratios for Equal Temperament and Pure Harmonic Series
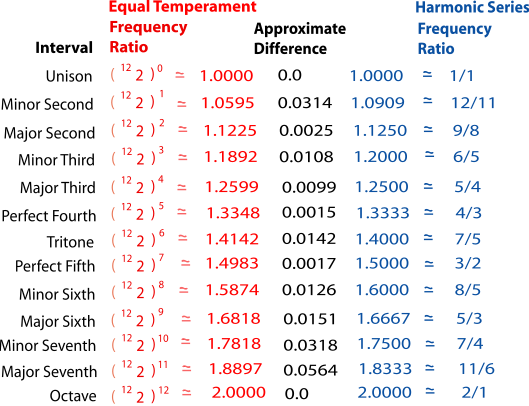
Except for the unison and the octave, none of the ratios for equal temperament are exactly the same as for the pure interval. Many of them are reasonably close, though. In particular, perfect fourths and fifths and major thirds are not too far from the pure intervals. The intervals that are the furthest from the pure intervals are the major seventh, minor seventh, and minor second (intervals that are considered dissonant anyway).
Because equal temperament is now so widely accepted as standard tuning, musicians do not usually even speak of intervals in terms of ratios. Instead, tuning itself is now defined in terms of equal-temperament, with tunings and intervals measured in cents. A cent is 1/100 (the hundredth root) of an equal-temperament semitone. In this system, for example, the major whole tone discussed above measures 204 cents, the minor whole tone 182 cents, and a pure fifth is 702 cents.
Why is a cent the hundredth root of a semitone, and why is a semitone the twelfth root of an octave? If it bothers you that the ratios in equal temperament are roots, remember the pure octaves and fifths of the harmonic series.
Figure 6.6. Frequency Relationships

Every octave has the same frequency ratio; the higher note will have 2 times the frequency of the lower note. So if you go up another octave from there (another 2 times), that note must have 2 x 2, or 4 times the frequency of the lowest note. The next octave takes you up 2 times higher than that, or 8 times the frequency of the first note, and so on.
In just the same way, in every perfect fifth, the higher note will have a frequency one and a half (3/2) times the lower note. So to find out how much higher the frequency is after a series of perfect fifths, you would have to multiply (not add) by one and a half (3/2) every time you went up another perfect fifth.
All intervals work in this same way. So, in order for twelve semitones (half steps) to equal one octave, the size of a half step has to be a number that gives the answer "2" (the size of an octave) when you multiply it twelve times: in other words, the twelfth root of two. And in order for a hundred cents to equal one semitone, the size of a cent must be the number that, when you multiply it 100 times, ends up being the same size as a semitone; in other words, the hundredth root of the twelfth root of two. This is one reason why most musicians prefer to talk in terms of cents and intervals instead of frequencies.
One well-known result of tempered tunings is the aural phenomenon known as beats. As mentioned above, in a pure interval the sound waves have frequencies that are related to each other by very simple ratios. Physically speaking, this means that the two smooth waves line up together so well that the combined wave - the wave you hear when the two are played at the same time - is also a smooth and very steady wave. Tunings that are slightly off from the pure interval, however, will result in a combined wave that has an extra bumpiness in it. Because the two waves are each very even, the bump itself is very even and regular, and can be heard as a "beat" - a very regular change in the intensity of the sound. The beats are so regular, in fact, that they can be timed; for equal temperament they are on the order of a beat per second in the mid range of a piano. A piano tuner works by listening to and timing these beats, rather than by being able to "hear" equal temperament intervals precisely.
It should also be noted that some music traditions around the world do not use the type of precision tunings described above, not because they can't, but because of an aesthetic preference for wide tuning. In these traditions, the sound of many people playing precisely the same pitch is considered a thin, uninteresting sound; the sound of many people playing near the same pitch is heard as full, lively, and more interesting.
Some music traditions even use an extremely precise version of wide tuning. The gamelan orchestras of southeast Asia, for example, have an aesthetic preference for the "lively and full" sounds that come from instruments playing near, not on, the same pitch. In some types of gamelans, pairs of instruments are tuned very precisely so that each pair produces beats, and the rate of the beats is the same throughout the entire range of that gamelan. Long-standing traditions allow gamelan craftsmen to reliably produce such impressive feats of tuning.
As of this writing:
-
The Just Intonation Network has much information about Just Intonation, including some audio examples.
-
Kyle Gann's An Introduction to Historical Tunings is a good source about both the historical background and more technical information about various tunings. It also includes some audio examples.
-
The Huygens-Fokker Foundation has a very large on-line bibliography of tuning and temperament.
-
Musemath has several animations illustrating equal temperament and the math necessary to understand it.
-
Alfredo Capurso, a researcher in Italy, has developed the Circular Harmonic System (c.ha.s), a tempered tuning system that solves the wolf fifth problem by adjusting the size of the octave as well as the fifth. It also provides an algorithm for generating microtonal scales. You can read about it at the Circular Harmonic System website or download apaper on the subject. You can also listen to piano performances using this tuning by searching for "CHAS tuning" at YouTube.
6.1. Ear Training*
When musicians talk about ear, they don't mean the sense organ itself so much as the brain's ability to perceive, distinguish, and understand what the ear has heard. The term ear training refers to teaching musicians to recognize information about notes and chords just by hearing them.
A few people have what is called perfect pitch or absolute pitch. These people, when they hear music, can tell you exactly what they are hearing: the G above middle C, for example, or the first inversion of an F minor chord. A few musicians with particularly perceptive ears can even tell you that a piano is tuned a few cents higher than the one that they play at home. This is an unusual skill that even most trained musicians do not have, and research seems to suggest that if you don't have it at a very early age, you cannot develop it. (For more on this subject, you may want to look up Robert Jourdain's Music, the Brain, and Ecstasy: How Music Captures our Imagination.)
However, most musicians can be trained to recognize relative pitch. In other words, if you play two notes, they can tell you that one of them is a major third higher than the other. If you play four chords in a row, they can tell you that you played a tonic-subdominant-dominant seventh-tonic (I-IV-V7-I) chord progression.
Fortunately, having relative pitch is good enough, and for many musicians may even be more useful than perfect pitch, because of the way Western music is conceived. Since all major keys are so similar, a piece in a major key will sound almost exactly the same whether you play it in C major or D major. The thing that matters is not what note you start on, but how all the notes are related to each other and to the "home" note (the tonic) of the key. If someone really wants the piece to be in a different key (because it's easier to sing or play in that key, or just because they want it to sound higher or lower), the whole thing can be transposed, but the only difference that would make (in the sound) is that the entire piece will sound higher or lower. Most listeners would not even notice the difference, unless you played it in both keys, one right after the other.
All minor keys are also heard by most listeners as interchangeable, but there are important differences between major keys and minor keys. In fact, the differences in sound between a major key and a minor key is one of the first differences that a musician should be able to hear. If you would like to see whether your "ear" can recognize the difference between major and minor keys, please try the listening exercise in Major Keys and Scales.
So, you often don't need to know exactly what notes or chords are being played. Simply having an ear well-trained in "relative pitch" is extremely useful in many ways. Guitar and piano players can figure out chord progressions just by listening to them, and then play the progressions in their favorite keys. Other instrumentalists can play a favorite tune without a written copy of it, just by knowing what the interval to the next note must be. Composers and music arrangers can jot down a piece of music without having to "pick it out" on an instrument to find the notes and chords they want. And of course, ear training is crucial to any musician who wants to play jazz or any type of improvisation. Given a well-trained "ear", any musical idea that you "hear" in your head, you can play. And ear training is also crucial for those interested in music theory, musicology, or just being able to write down a tune accurately.
As with all other musical skills, there are many different levels and kinds of proficiency. One musician may be very good at "playing by ear", but may not even read music and cannot name intervals or write the music down. Another may be very good at "taking dictation" (writing down the music they hear), and yet feel unable to do jazz improvisation. As always, the key is to practice the particular skills that you want to develop.
Tuning
This is the most basic ear training skill, crucial to being able to play music that people will want to hear.
Suggestions
-
At the beginner level, work with a skilled musician who can teach you how to tune your instrument and help you identify and fix tuning problems.
-
Play with other musicians often. (Playing along with recordings does not teach good tuning skills.) Don't just tune at the beginning of rehearsals and performances. Listen at all times and be ready to retune any note whenever necessary.
-
Spend as much time as necessary tuning whenever you play. Do not (knowingly) practice while out of tune; if you do, it will slow down your ear training tremendously. Whenever possible, until you are good at tuning, get someone else to help you tune every time you play.
-
Practice tuning quickly and accurately. Learn any alternate fingerings and other "tricks" available on your instrument for fine-tuning each note as you play.
Playing Chords By Ear
For instruments that play chordal accompaniments, this is an incredibly useful skill.
Suggestions
-
You do not have to learn to read music to be able to do this, but it is very helpful to know a little bit about music theory so that you can predict which chords are most likely to happen in a song. Try starting with Beginning Harmonic Analysis.
-
EarMaster includes 3 activities for harmonic ear training: Chord Identification, Chord Inversions, and Chord Progressions (including cadences). Training with those activities will help you develop your abilities to play chords and other harmonic content by ear.
-
Really listen to the chord progressions to the songs you do know. What do they sound like? Play the same progressions in different keys and listen to how that does and also does not change the sound of the progression. Change the bass notes of the chords to see how that changes the sound of the progression to your ears. Change fingerings and chord voicings, and again listen carefully to how that changes the sound to your ears.
-
Practice figuring out the chords to familiar songs (that you don't know the chords to). For songs that you do know the chords to, try playing them in an unfamiliar key, or see if you can change or add chords to make a new harmony that still fits the melody.
-
A teacher who understands harmony can help tremendously with this particular skill. Even if you don't normally take lessons, you might want to consider having a series of lessons on this. Find a teacher who is willing and able to teach you specifically about harmony and typical chord progressions.
Playing Tunes by Ear
This is fun to be able to do, makes it easy to increase your repertoire, and is an important step in being able to improvise.
Suggestions
-
Just do it! The best way to learn this skill is to spend some of your practice time trying to play tunes you know and like.
-
EarMaster's Melody Imitation activity is an efficient and easy way to power-train your ear and pitch accuracy. In that activity, EarMaster plays a melody that you have to sing back. The software evaluates the accuracy of your performance in real-time and increases the difficulty of the exercises as you become better at singing back tunes.
-
Once you start getting good at this, see how quickly you can get a new tune down. How few mistakes can you make the first time you try it? Can you "recover" quickly from a mistake by making it sound like a bit of improvisation?
-
If you play a melody instrument (one that plays only one note at a time), there are different bits of information that help you recognize what the next note will be: how far it is from the note you are on (see Interval), where it is in the key (see Beginning Harmonic Analysis) or where it is in the chord (see Triads). These three things are all related to each other, of course - and a musician with a well-trained ear will be aware of all of them, at least subconsciously - but you may find at first that one works better for you than the others. You may want to experiment: is it easier for you to think of the next note as being a perfect fourth higher than the note you are on, or as being the root of the chord, or as being the fifth note in the scale of the key?
Improvisation
This is the skill you need for jazz. Blues, rock, and many Non-Western traditions also use improvisation.
Suggestions
-
Know your scales and arpeggios. A good improviser, given the name of a chord, can quickly play not only the notes of the chord but also the scale implied by the chord. Any decent book on playing jazz, or any teacher familiar with jazz, will introduce the student to these chords and scales.
-
There are now many book/CD combinations available to help the beginning improviser in many different genres and on many different instruments. A good book of this type will give the student a chance to improvise on many familiar tunes, and some also introduce the music theory involved. At the time of this writing, one source of a large variety of such books was jazzbooks.com. The exercises at the petersax site mentioned above would also be useful for the beginning improviser.
-
Listen to jazz often. Listen to the improvisers you admire, and if a particular solo really appeals to you, listen to it many times, find the notes on your instrument, and then try writing it down as accurately as you can. Many famous improvisors, when interviewed, mention how useful it was to them to learn from other soloists by transcribing their solos in this way.
-
Figure out how to play your favorite jazz (or blues or rock) licks (short motives that show up in many pieces in the same genre) on your instrument. Practice stringing them together in ways that make sense to you, but are different from what you've heard. Add your own variations.
-
Find a teacher who is familiar with the type of improvisation you want to learn, join a jazz band, and/or get together with other musicians who also want to practise improvisation and take turns playing background/rhythm for each other.
Recognizing Intervals and Writing Music Down
This is the skill that allowed Beethoven to continue composing masterpieces even after he became deaf. If you are interested in composing, arranging, music theory, musicology, or just being able to write down a tune quickly and accurately, you'll want to be able to make that quick connection between what you hear and written music.
Suggestions
-
Before you can do this, you must know your major and minor keys and scales and your Intervals. You may also want to understand Transposition, since you may find it easier to work in some keys than in others.
-
EarMaster contains 3 activities that will help you get better at recognizing, transcribing and playing intervals: Interval Comparison, Interval Identification, and Interval Singing.
-
Once again, practice is the best way to become good at this. Start with tunes that you know well, but don't know what the (written) notes are. Listen to them in your head (or play a recording) while trying to write them down. Then play what you have written, noticing where you were correct and where you made mistakes. Which intervals are you good at hearing? Which do you have trouble identifying? Do you often mistake one particular interval for another? Do you tend to identify a note by its interval from the previous note or by its place in the chord or in the key? Answering these questions will help you improve more quickly.
-
Some people find it easier to learn to recognize intervals if they associate each interval with a familiar tune. (For example, in the familiar song from The Sound of Music that begins "Do, a deer, a female deer...", all the intervals in the phrase "a female deer" are major thirds, and every interval in the phrase "someday I'll wish upon a star" in the song "Somewhere Over the Rainbow" is a minor third.) The tune should be very familiar, so when trying to hear a tritone, some people will prefer thinking of the beginning of "The Simpsons" theme; others will prefer the beginning of "Maria" from West Side Story. If you think this method will work for you, try playing the interval you are having trouble hearing, and see what tune it reminds you of.
-
On EarMaster's website, you will find a comprehensive list of reference songs for interval memorization. Each melody is illustrated by a YouTube video, and the page lets you compile your own list of songs in a ready-to-print layout: Interval Song Chart Generator.





