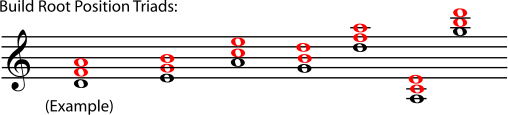
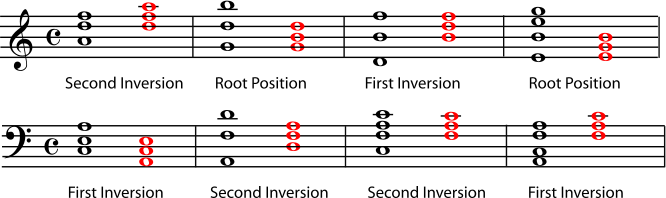
5.2. Naming Triads*
The position that a chord is in does make a difference in how it sounds, but it is a fairly small difference. Listen to a G major chord in three different positions.
Figure 5.9.

A much bigger difference in the chord's sound comes from the intervals between the root-position notes of the chord. For example, if the B in one of the chords above was changed to a B flat, you would still have a G triad, but the chord would now sound very different. So chords are named according to the intervals between the notes when the chord is in root position. Listen to four different G chords.
Figure 5.10.

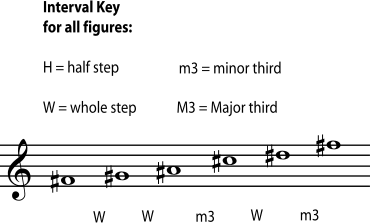
The most commonly used triads form major chords and minor chords. All major chords and minor chords have an interval of a perfect fifth between the root and the fifth of the chord. A perfect fifth (7 half-steps) can be divided into a major third (4 half-steps) plus a minor third (3 half-steps). If the interval between the root and the third of the chord is the major third (with the minor third between the third and the fifth of the chord), the triad is a major chord. If the interval between the root and the third of the chord is the minor third (and the major third is between the third and fifth of the chord), then the triad is a minor chord. Listen closely to a major triad and a minor triad.
Example 5.3.
Figure 5.11.

Example 5.4.
Figure 5.12. Some Major and Minor Triads

Because they don't contain a perfect fifth, augmented and diminished chords have an unsettled feeling and are normally used sparingly. An augmented chord is built from two major thirds, which adds up to an augmented fifth. A diminished chord is built from two minor thirds, which add up to a diminished fifth. Listen closely to an augmented triad and a diminished triad.
Example 5.5.
Figure 5.15. Some Augmented and Diminished Triads

Notice that you can't avoid double sharps or double flats by writing the note on a different space or line. If you change the spelling of a chord's notes, you have also changed the chord's name. For example, if, in an augmented G sharp major chord, you rewrite the D double sharp as an E natural, the triad becomes an E augmented chord.
Figure 5.18.

You can put the chord in a different position or add more of the same-named notes at other octaves without changing the name of the chord. But changing the note names or adding different-named notes, will change the name of the chord. Here is a summary of the intervals in triads in root position.
Figure 5.19.

Exercise 5.2.5. (Go to Solution)
Now see if you can identify these chords that are not necessarily in root position. Rewrite them in root position first if that helps.
Figure 5.20.

Solutions to Exercises
5.1. Triads*
Harmony in Western music is based on triads. Triads are simple three-note chords built of thirds.
Figure 5.1. Triads in Root Position

The chords in Figure 5.1 are written in root position, which is the most basic way to write a triad. In root position, the root, which is the note that names the chord, is the lowest note. The third of the chord is written a third higher than the root, and the fifth of the chord is written a fifth higher than the root (which is also a third higher than the third of the chord). So the simplest way to write a triad is as a stack of thirds, in root position.
The type of interval or chord - major, minor, diminished, etc., is not important when you are determining the position of the chord. To simplify things, all notes in the examples and exercises below are natural, but it would not change their position at all if some notes were sharp or flat. It would, however, change the name of the triad - see Naming Triads.
Any other chord that has the same-named notes as a root position chord is considered to be essentially the same chord in a different position. In other words, all chords that have only D naturals, F sharps, and A naturals, are considered D major chords.
But if you change the pitch or spelling of any note in the triad, you have changed the chord (see Naming Triads). For example, if the F sharps are written as G flats, or if the A's are sharp instead of natural, you have a different chord, not an inversion of the same chord. If you add notes, you have also changed the name of the chord (see Beyond Triads). You cannot call one chord the inversion of another if either one of them has a note that does not share a name (for example "F sharp" or "B natural") with a note in the other chord.
If the third of the chord is the lowest note, the chord is in first inversion. If the fifth of the chord is the lowest note, the chord is in second inversion. A chord in second inversion may also be called a six-four chord, because the intervals in it are a sixth and a fourth.
Figure 5.3.

It does not matter how far the higher notes are from the lowest note, or how many of each note there are (at different octaves or on different instruments); all that matters is which note is lowest. (In fact, one of the notes may not even be written, only implied by the context of the chord in a piece of music. A practiced ear will tell you what the missing note is; we won't worry about that here.) To decide what position a chord is in, move the notes to make a stack of thirds and identify the root.
Example 5.1.
Figure 5.4.

Example 5.2.
Figure 5.5.

Exercise 5.1.2. (Go to Solution)
Rewrite each chord in root position, and name the original position of the chord.
Figure 5.6.

Solutions to Exercises
4.8. Scales that aren't Major or Minor*
Sounds - ordinary, everyday "noises" - come in every conceivable pitch and groups of pitches. In fact, the essence of noise, "white noise", is basically every pitch at once, so that no particular pitch is heard.
One of the things that makes music pleasant to hear and easy to "understand" is that only a few of all the possible pitches are used. But not all pieces of music use the same set of pitches. In order to be familiar with the particular notes that a piece of music is likely to use, musicians study scales.
The set of expected pitches for a piece of music can be arranged into a scale. In a scale, the pitches are usually arranged from lowest to highest (or highest to lowest), in a pattern that usually repeats within every octave.
In some kinds of music, the notes of a particular scale are the only notes allowed in a given piece of music. In other music traditions, notes from outside the scale (accidentals) are allowed, but are usually much less common than the scale notes.
The set of pitches, or notes, that are used, and their relationships to each other, makes a big impact on how the music sounds. For example, for centuries, most Western music has been based on major and minor scales. That is one of the things that makes it instantly recognizable as Western music. Much (though not all) of the music of eastern Asia, on the other hand, was for many centuries based on pentatonic scales, giving it a much different flavor that is also easy to recognize.
Some of the more commonly used scales that are not major or minor are introduced here. Pentatonic scales are often associated with eastern Asia, but many other music traditions also use them. Blues scales, used in blues, jazz, and other African-American traditions, grew out of a compromise between European and African scales. Some of the scales that sound "exotic" to the Western ear are taken from the musical traditions of eastern Europe, the Middle East, and western Asia. Microtones can be found in some traditional musics (for example, Indian classical music) and in some modern art music.
Some music traditions, such as Indian and medieval European, use modes or ragas, which are not quite the same as scales. Please see Modes and Ragas.
The Western musical tradition that developed in Europe after the middle ages is based on major and minor scales, but there are other scales that are a part of this tradition.
In the chromatic scale, every interval is a half step. This scale gives all the sharp, flat, and natural notes commonly used in all Western music. It is also the twelve-tone scale used by twentieth-century composers to create their atonal music. Young instrumentalists are encouraged to practice playing the chromatic scale in order to ensure that they know the fingerings for all the notes. Listen to a chromatic scale.
Figure 4.65. Chromatic Scale

In a whole tone scale, every interval is a whole step. In both the chromatic and the whole tone scales, all the intervals are the same. This results in scales that have no tonal center; no note feels more or less important than the others. Because of this, most traditional and popular Western music uses major or minor scales rather than the chromatic or whole tone scales. But composers who don't want their music to have a tonal center (for example, many composers of "modern classical" music) often use these scales. Listen to a whole tone scale.
Figure 4.66. A Whole Tone Scale

Exercise 4.8.1. (Go to Solution)
There is basically only one chromatic scale; you can start it on any note, but the pitches will end up being the same as the pitches in any other chromatic scale. There are basically two possible whole tone scales. Beginning on a b, write a whole tone scale that uses a different pitches than the one in Figure 4.66.
Exercise 4.8.2. (Go to Solution)
Now write a whole tone scale beginning on an a flat. Is this scale essentially the same as the one in Figure 4.75 or the one in Figure 4.66?
In Western music, there are twelve pitches within each octave. (The thirteenth note starts the next octave.) But in a tonal piece of music only seven of these notes, the seven notes of a major or minor scale, are used often.
In a pentatonic scale, only five of the possible pitches within an octave are used. (So the scale will repeat starting at the sixth tone.) The most familiar pentatonic scales are used in much of the music of eastern Asia. You may be familiar with the scale in Figure 4.67 as the scale that is produced when you play all the "black keys" on a piano keyboard.
Figure 4.67. A Familiar Pentatonic Scale
Listen to the black key pentatonic scale. Like other scales, this pentatonic scale is transposable; you can move the entire scale up or down by a half step or a major third or any interval you like. The scale will sound higher or lower, but other than that it will sound the same, because the pattern of intervals between the notes (half steps, whole steps, and minor thirds) is the same. (For more on intervals, see Half Steps and Whole Steps and Interval. For more on patterns of intervals within scales, see Major Scales and Minor Scales.) Now listen to a transposed pentatonic scale.
But this is not the only possible type of pentatonic scale. Any scale that uses only five notes within one octave is a pentatonic scale. The following pentatonic scale, for example, is not simply another transposition of the "black key" pentatonic scale; the pattern of intervals between the notes is different. Listen to this different pentatonic scale.
Figure 4.69. Different Pentatonic Scale

The point here is that music based on the pentatonic scale in Figure 4.67 will sound very different from music based on the pentatonic scale in Figure 4.69, because the relationships between the notes are different, much as music in a minor key is noticeably different from music in a major key. So there are quite a few different possible pentatonic scales that will produce a recognizably "unique sound", and many of these possible five-note scales have been named and used in various music traditions around the world.
Exercise 4.8.3. (Go to Solution)
To get a feeling for the concepts in this section, try composing some short pieces using the pentatonic scales given in Figure 4.67 and in Figure 4.69. You may use more than one octave of each scale, but use only one scale for each piece. As you are composing, listen for how the constraints of using only those five notes, with those pitch relationships, affect your music. See if you can play your Figure 4.67 composition in a different key, for example, using the scale in Figure 4.68.
Any scale will list a certain number of notes within an octave. For major and minor scales, there are seven notes; for pentatonic, five; for a chromatic scale, twelve. Although some divisions are more common than others, any division can be imagined, and many are used in different musical traditions around the world. For example, the classical music of India recognizes twenty-two different possible pitches within an octave; each raga uses five, six, or seven of these possible pitches. (Please see Indian Classical Music: Tuning and Ragas for more on this.) And there are some traditions in Africa that use six or eight notes within an octave. Listen to one possible eight-tone, or octatonic scale.
Figure 4.70. An Octatonic Scale

Many Non-Western traditions, besides using different scales, also use different tuning systems; the intervals in the scales may involve quarter tones (a half of a half step), for example, or other intervals we don't use. Even trying to write them in common notation can be a bit misleading.
Microtones are intervals smaller than a half step. Besides being necessary to describe the scales and tuning systems of many Non-Western traditions, they have also been used in modern Western classical music, and are also used in African-American traditions such as jazz and blues. As of this writing, the Huygens-Fokker Foundation was a good place to start looking for information on microtonal music.
Blues scales are closely related to pentatonic scales. (Some versions are pentatonic.) Rearrange the pentatonic scale in Figure 4.68 above so that it begins on the C, and add an F sharp in between the F and G, and you have a commonly used version of the blues scale. Listen to this blues scale.
Figure 4.71.

Many music traditions do not use scales. The most familiar of these to the Western listener are medieval chant and the classical music of India. In these and other modal traditions, the rules for constructing a piece of music are quite different than the rules for music that is based on a scale. Please see Modes and Ragas for more information.
There are many, many other possible scales that are not part of the major-minor system. Some, like pentatonic and octatonic scales, have fewer or more notes per octave, but many have seven tones, just as a major scale does. A scale may be chosen or constructed by a composer for certain intriguing characteristics, for the types of melodies or harmonies that the scale enables, or just for the interesting or pleasant sound of music created using the scale.
For example, one class of scales that intrigues some composers is symmetrical scales. The chromatic scale and whole tone scales fall into this category, but other symmetrical scales can also be constructed. A diminished scale, for example, not only has the "symmetrical" quality; it is also a very useful scale if, for example, you are improvising a jazz solo over diminished chords.
Figure 4.72. A Diminished Scale

Some scales are loosely based on the music of other cultures, and are used when the composer wants to evoke the music of another place or time. These scales are often borrowed from Non-western traditions, but are then used in ways typical of Western music. Since they usually ignore the tuning, melodic forms, and other aesthetic principles of the traditions that they are borrowed from, such uses of "exotic" scales should not be considered accurate representations of those traditions. There are examples in world music, however, in which the Non-western scale or mode is used in an authentic way. Although there is general agreement about the names of some commonly used "exotic" scales, they are not at all standardized. Often the name of a scale simply reflects what it sounds like to the person using it, and the same name may be applied to different scales, or different names to the same scale.
Figure 4.73. Some "Exotic" Scales

You may want to experiment with some of the many scales possible. Listen to one version each of: "diminished" scale, "enigmatic" scale, "Romanian" Scale, "Persian" scale and "Hungarian Major" Scale. For even more possibilities, try a web search for "exotic scales"; or try inventing your own scales and using them in compositions and improvisations.
Figure 4.74. An "Enigmatic" Scale

Solutions to Exercises
Solution to Exercise 4.8.1. (Return to Exercise)
Figure 4.75.

Solution to Exercise 4.8.2. (Return to Exercise)
Figure 4.76.

Assuming that octaves don't matter - as they usually don't in Western music theory, this scale shares all of its possible pitches with the scale in Figure 4.66.
Solution to Exercise 4.8.3. (Return to Exercise)
If you can, have your teacher listen to your compositions.
4.7. The Circle of Fifths*
The circle of fifths is a way to arrange keys to show how closely they are related to each other.
Figure 4.58. Circle of Fifths
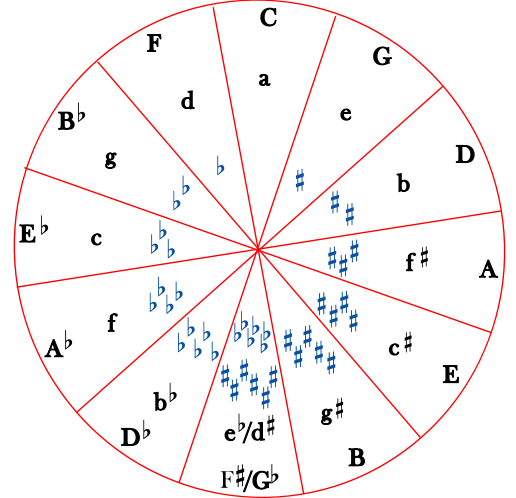
Keys are not considered closely related to each other if they are near each other in the chromatic scale (or on a keyboard). What makes two keys "closely related" is having similar key signatures. So the most closely related key to C major, for example, is A minor, since they have the same key signature (no sharps and no flats). This puts them in the same "slice" of the circle. The next most closely related keys to C major would be G major (or E minor), with one sharp, and F major (or D minor), with only one flat. The keys that are most distant from C major, with six sharps or six flats, are on the opposite side of the circle.
The circle of fifths gets its name from the fact that as you go from one section of the circle to the next, you are going up or down by an interval of a perfect fifth. If you go up a perfect fifth (clockwise in the circle), you get the key that has one more sharp or one less flat; if you go down a perfect fifth (counterclockwise), you get the key that has one more flat or one less sharp. Since going down by a perfect fifth is the same as going up by a perfect fourth, the counterclockwise direction is sometimes referred to as a "circle of fourths". (Please review inverted intervals if this is confusing.)
If you want to experiment with the Circle of Fifths, we recommend that you try this excellent interactive Circle of Fifths.
Example 4.10.
The key of D major has two sharps. Using the circle of fifths, we find that the most closely related major keys (one in each direction) are G major, with only one sharp, and A major, with three sharps. The relative minors of all of these keys (B minor, E minor, and F sharp minor) are also closely related to D major.
Exercise 4.7.1. (Go to Solution)
What are the keys most closely related to E flat major? To A minor?
If you do not know the order of the sharps and flats, you can also use the circle of fifths to find these. The first sharp in a key signature is always F sharp; the second sharp in a key signature is always (a perfect fifth away) C sharp; the third is always G sharp, and so on, all the way to B sharp.
The first flat in a key signature is always B flat (the same as the last sharp); the second is always E flat, and so on, all the way to F flat. Notice that, just as with the key signatures, you add sharps or subtract flats as you go clockwise around the circle, and add flats or subtract sharps as you go counterclockwise.
Figure 4.60. Adding Sharps and Flats to the Key Signature
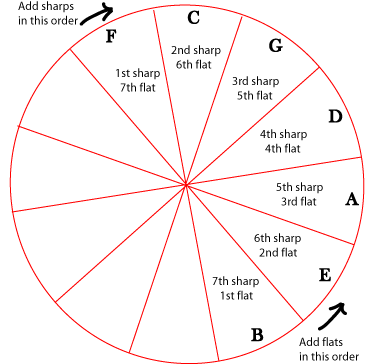
Exercise 4.7.3. (Go to Solution)
Figure 4.58 shows that D major has 2 sharps; Figure 4.60 shows that they are F sharp and C sharp. After D major, name the next four sharp keys, and name the sharp that is added with each key.
Exercise 4.7.4. (Go to Solution)
E minor is the first sharp minor key; the first sharp added in both major and minor keys is always F sharp. Name the next three sharp minor keys, and the sharp that is added in each key.
Exercise 4.7.5. (Go to Solution)
After B flat major, name the next four flat keys, and name the flat that is added with each key.
Solutions to Exercises
Solution to Exercise 4.7.1. (Return to Exercise)
E flat major (3 flats):
-
B flat major (2 flats)
-
A flat major (4 flats)
-
C minor (3 flats)
-
G minor (2 flats)
-
F minor (4 flats)
A minor (no sharps or flats):
-
E minor (1 sharp)
-
D minor (1 flat)
-
C major (no sharps or flats)
-
G major (1 sharp)
-
F major (1 flat)
Solution to Exercise 4.7.3. (Return to Exercise)
-
A major adds G sharp
-
E major adds D sharp
-
B major adds A sharp
-
F sharp major adds E sharp
Figure 4.62.

Solution to Exercise 4.7.4. (Return to Exercise)
-
B minor adds C sharp
-
F sharp minor adds G sharp
-
C sharp minor adds D sharp
Figure 4.63.

Solution to Exercise 4.7.5. (Return to Exercise)
-
E flat major adds A flat
-
A flat major adds D flat
-
D flat major adds G flat
-
G flat major adds C flat
Figure 4.64.

4.6. Harmonic Series II: Harmonics, Intervals, and Instruments*
The names of the various intervals, and the way they are written on the staff, are mostly the result of a long history of evolving musical notation and theory. But the actual intervals - the way the notes sound - are not arbitrary accidents of history. Like octaves, the other intervals are also produced by the harmonic series. Recall that the frequencies of any two pitches that are one octave apart have a 2:1 ratio. (See Harmonic Series I to review this.) Every other interval that musicians talk about can also be described as having a particular frequency ratio. To find those ratios, look at a harmonic series written in common notation.
Figure 4.53. A Harmonic Series Written as Notes

Look at the third harmonic in Figure 4.53. Its frequency is three times the frequency of the first harmonic (ratio 3:1). Remember, the frequency of the second harmonic is two times that of the first harmonic (ratio 2:1). In other words, there are two waves of the higher C for every one wave of the lower C, and three waves of the third-harmonic G for every one wave of the fundamental. So the ratio of the frequencies of the second to the third harmonics is 2:3. (In other words, two waves of the C for every three of the G.) From the harmonic series shown above, you can see that the interval between these two notes is a perfect fifth. The ratio of the frequencies of all perfect fifths is 2:3.
Exercise 4.6.1. (Go to Solution)
-
The interval between the fourth and sixth harmonics (frequency ratio 4:6) is also a fifth. Can you explain this?
-
What other harmonics have an interval of a fifth?
-
Which harmonics have an interval of a fourth?
-
What is the frequency ratio for the interval of a fourth?
If you have been looking at the harmonic series above closely, you may have noticed that some notes that are written to give the same interval have different frequency ratios. For example, the interval between the seventh and eighth harmonics is a major second, but so are the intervals between 8 and 9, between 9 and 10, and between 10 and 11. But 7:8, 8:9, 9:10, and 10:11, although they are pretty close, are not exactly the same. In fact, modern Western music uses the equal temperament tuning system, which divides the octave into twelve notes that are equally far apart. (They do have the same frequency ratios, unlike the half steps in the harmonic series.) The positive aspect of equal temperament (and the reason it is used) is that an instrument will be equally in tune in all keys. The negative aspect is that it means that all intervals except for octaves are slightly out of tune with regard to the actual harmonic series. For more about equal temperament, see Tuning Systems. Interestingly, musicians have a tendency to revert to true harmonics when they can (in other words, when it is easy to fine-tune each note). For example, an a capella choral group, or a brass ensemble, may find themselves singing or playing perfect fourths and fifths, "contracted" major thirds and "expanded" minor thirds, and half and whole steps of slightly varying sizes.
The harmonic series is particularly important for brass instruments. A pianist or xylophone player only gets one note from each key. A string player who wants a different note from a string holds the string tightly in a different place. This basically makes a vibrating string of a new length, with a new fundamental.
But a brass player, without changing the length of the instrument, gets different notes by actually playing the harmonics of the instrument. Woodwinds also do this, although not as much. Most woodwinds can get two different octaves with essentially the same fingering; the lower octave is the fundamental of the column of air inside the instrument at that fingering. The upper octave is the first harmonic.
In some woodwinds, such as the clarinet, the upper "octave" may actually be the third harmonic rather than the second, which complicates the fingering patterns of these instruments. Please see Standing Waves and Wind Instruments for an explanation of this phenomenon.
It is the brass instruments that excel in getting different notes from the same length of tubing. The sound of a brass instruments starts with vibrations of the player's lips. By vibrating the lips at different speeds, the player can cause a harmonic of the air column to sound instead of the fundamental. Thus a bugle player can play any note in the harmonic series of the instrument that falls within the player's range. Compare these well-known bugle calls to the harmonic series above.
Figure 4.54. Bugle Calls

For centuries, all brass instruments were valveless. A brass instrument could play only the notes of one harmonic series. (An important exception was the trombone and its relatives, which can easily change their length and harmonic series using a slide.) The upper octaves of the series, where the notes are close enough together to play an interesting melody, were often difficult to play, and some of the harmonics sound quite out of tune to ears that expect equal temperament. The solution to these problems, once brass valves were perfected, was to add a few valves to the instrument; three is usually enough. Each valve opens an extra length of tube, making the instrument a little longer, and making available a whole new harmonic series. Usually one valve gives the harmonic series one half step lower than the valveless intrument; another, one whole step lower; and the third, one and a half steps lower. The valves can be used in combination, too, making even more harmonic series available. So a valved brass instrument can find, in the comfortable middle of its range (its middle register), a valve combination that will give a reasonably in-tune version for every note of the chromatic scale. (For more on the history of valved brass, see History of the French Horn. For more on how and why harmonics are produced in wind instruments, please see Standing Waves and Wind Instruments)
Trombones still use a slide instead of valves to make their instrument longer. But the basic principle is still the same. At each slide "position", the instrument gets a new harmonic series. The notes in between the positions aren't part of the chromatic scale, so they are usually only used for special effects like glissandos (sliding notes).
Figure 4.55. Overlapping Harmonic Series in Brass Instruments

Exercise 4.6.2. (Go to Solution)
Write the harmonic series for the instrument above when both the first and second valves are open. What new notes are added in the instrument's middle range? Are any notes still missing?
The French horn has a reputation for being a "difficult" instrument to play. This is also because of the harmonic series. Most brass instruments play in the first few octaves of the harmonic series, where the notes are farther apart and it takes a pretty big difference in the mouth and lips (the embouchure, pronounced AHM-buh-sher) to get a different note. The range of the French horn is higher in the harmonic series, where the notes are closer together. So very small differences in the mouth and lips can mean the wrong harmonic comes out.
String players also use harmonics, although not as much as brass players. Harmonics on strings have a very different timbre from ordinary string sounds. They give a quieter, thinner, more bell-like tone, and are usually used as a kind of ear-catching special-effect.
Normally a string player holds a string down very tightly. This shortens the length of the vibrating part of the string, in effect making a (temporarily) shorter vibrating string, which has its own full set of harmonics.
To "play a harmonic", the string is touched very, very lightly instead. The length of the string does not change. Instead, the light touch interferes with all of the vibrations that don't have a node at that spot.
Figure 4.56. String Harmonics
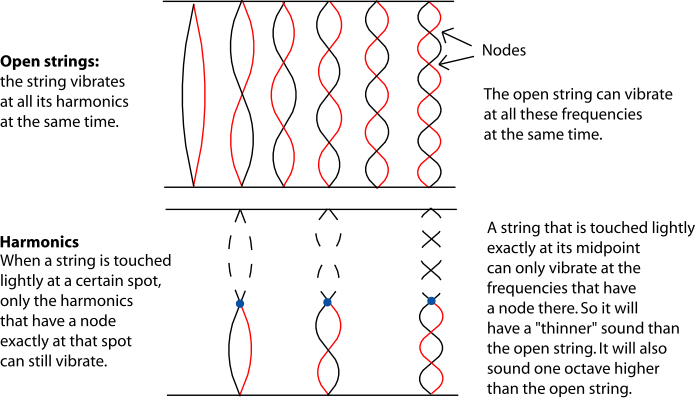
The thinner, quieter sound of "playing harmonics" is caused by the fact that much of the harmonic series is missing from the sound, which will of course affect the timbre. Lightly touching the string in most places will result in no sound at all. This technique only works well at places on the string where a main harmonic (one of the longer, louder lower-numbered harmonics) has a node. Some string players can get more harmonics by both holding the string down in one spot and touching it lightly in another spot, but this is an advanced technique.
Solutions to Exercises
Solution to Exercise 4.6.1. (Return to Exercise)
-
The ratio 4:6 reduced to lowest terms is 2:3. (In other words, they are two ways of writing the same mathematical relationship. If you are more comfortable with fractions than with ratios, think of all the ratios as fractions instead. 2:3 is just two-thirds, and 4:6 is four-sixths. Four-sixths reduces to two-thirds.)
-
Six and nine (6:9 also reduces to 2:3); eight and twelve; ten and fifteen; and any other combination that can be reduced to 2:3 (12:18, 14:21 and so on).
-
Harmonics three and four; six and eight; nine and twelve; twelve and sixteen; and so on.
-
3:4
Solution to Exercise 4.6.2. (Return to Exercise)
Opening both first and second valves gives the harmonic series one-and-a-half steps lower than "no valves".
Figure 4.57.